

We also show the benefits of our approach on a real-world public dataset sampled from a laboratory-based ecological experiment.Īrgyriou, A., Evgeniou, T., & Pontil, M. Experimental results, based on noisy data simulated from known SODEs, confirm that, compared to single-task learning, MTL is more effective for recovering the closed-form SODE, and the proposed nonconvexity ensures that it can be estimated with unbiasedness. Our proposal improves SODE identification by harnessing a nonconvex sparse matrix-structured penalty which takes into account the coupling feature as well as addresses the bias issue. But discovering an SODE is nontrivial, as dynamic systems are often nonlinear and the available data are noisy. The purpose of each task is to discover a single equation. To reduce such a bias, we propose a multitask learning (MTL) based penalty which can learn the closed-form SODE with unbiasedness. Furthermore, the convexity of the sparse penalty included in the learning criterion gives an SODE that is biased with respect to the true SODE. Omitting the coupling features of equations leads to SODEs that weakly identify the dynamic system. State-of-the-art approaches are based on sparse single-task learning, which means that each equation from the SODE is learned independently. With advances in sensor technology, large quantities of data can be sampled from dynamic systems, thus enabling the data-driven discovery of closed-form SODEs.
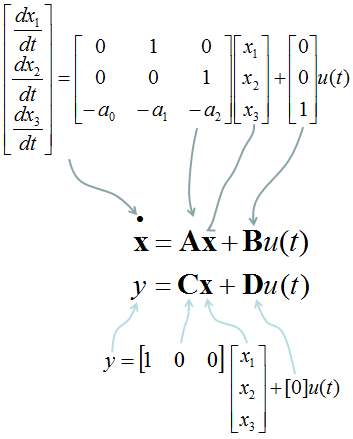
Although in certain cases the SODE can be written by domain experts, it is often unknown. A parameter can appear in multiple equations, and this parameter potentially links the equations to each other. This system consists of multiple equations, each of which relates the time derivative of a single parameter to several parameters. In physical sciences, dynamic systems are modeled using their parameters within governing equations that often form a system of ordinary differential equations (SODE).


 0 kommentar(er)
0 kommentar(er)
